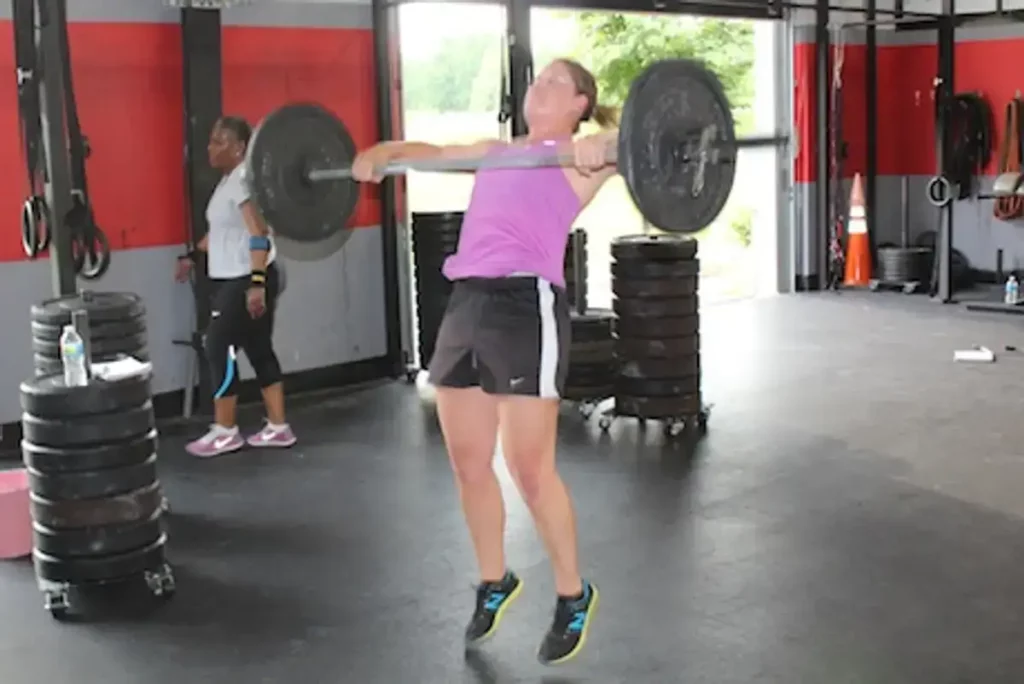



WOD: A. Deadlift: 4-3-2-1-1 E3MOM B. 10 rounds for time of: 15 deadlifts 135/95 15 hand release push ups
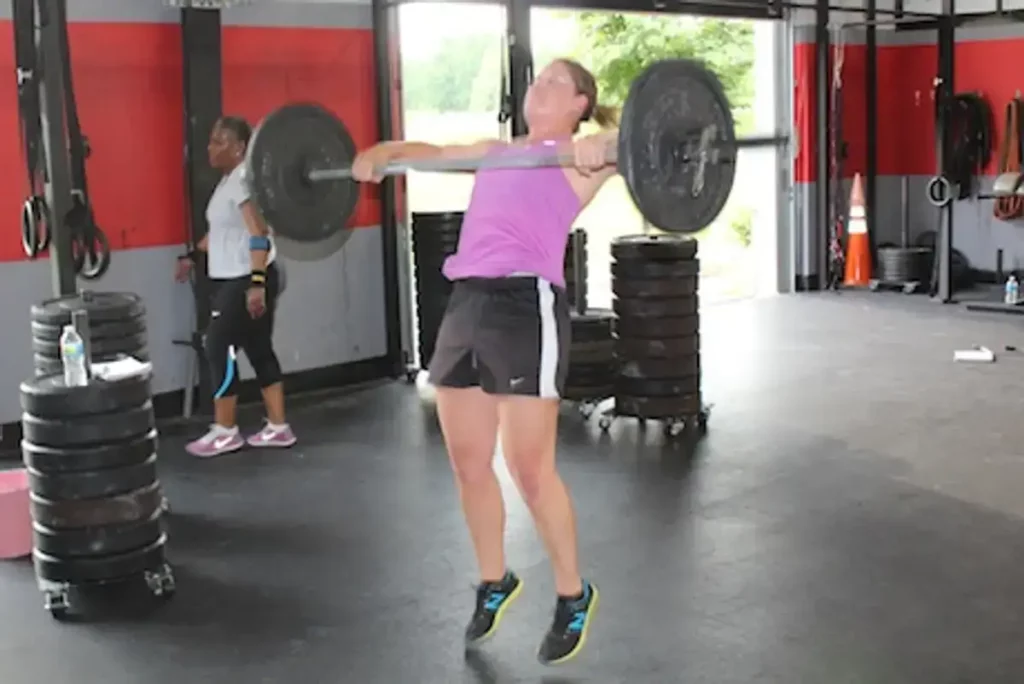



WOD: A. Deadlift: 4-3-2-1-1 E3MOM B. 10 rounds for time of: 15 deadlifts 135/95 15 hand release push ups
3050 Leeman Ferry Rd, Huntsville, Alabama 35801
GIVE US A CALL
(256) 408-5990
3050 Leeman Ferry Rd, Huntsville, Alabama 35801
(256) 408-5990